NumPy的知识与实践
 爱校码
爱校码
一、NumPy的用途
NumPy(Numerical Python)是 Python 语言的一个扩展程序库,是一个高效计算工具,不同于普通编程中变量计算,具有以下特点:
- 可以进行n维数组的高效计算,具有矢量运算能力,且快速,节省空间;
- 能进行线性代数、傅立叶变换等多种高效科学运算,可对整组数据进行快速运算的标准数学函数;
- 有丰富的随机数功能;
- 有丰富的数组处理功能,可以进行广播计算;
NumPy 为开放源代码并且由许多协作者共同维护开发。
二、NumPy使用基础
使用NumPy时,需要先行导入numpy包:
import numpy as np
之后就可以利用缩写的np使用numpy包了,在以下的讲述中,数组、矩阵都指的是ndarray对象(N 维数组对象)。
数组对象:
NumPy的数组类称为ndarray,也是N维数组的别名,它是一系列同类型数据的集合,以 0 下标开始对集合中的元素进行索引的。NumPy的基础计算对象是数组,NumPy的数组与Python的列表list不同,list中的元素可以是不同类型,而NumPy数组中的元素都为一种类型。
使用NumPy构建数组需要两个关键参数:shape(数组形状)和dtype(类型)
1.利用ndarray构造方法创建数组:
>>> import numpy as np
>>> a = np.ndarray(shape=(2,3),dtype=float)
>>> a
array([[5.50148290e+222, 5.34753902e+246, 8.50060723e-096],
[4.27255707e+180, 1.03471377e-259, 6.94168483e-310]])
>>>
其结果是一个2行3列的float类型的随机数组。当然更多维数组也可以:
>>> a = np.ndarray(shape=(2,3,5),dtype=float)
>>> a
array([[[ 1.28822975e-231, -1.29074164e-231, -7.90505033e-323,
0.00000000e+000, 2.12199579e-314],
[ 0.00000000e+000, 0.00000000e+000, 0.00000000e+000,
1.75871011e-310, 3.50977866e+064],
[ 0.00000000e+000, 3.97645035e-309, nan,
nan, 3.50977942e+064]],
[[ 1.13813711e-308, 0.00000000e+000, 0.00000000e+000,
-0.00000000e+000, 0.00000000e+000],
[ 2.12199579e-314, 0.00000000e+000, 0.00000000e+000,
0.00000000e+000, 1.75871011e-310],
[ 3.50977866e+064, 0.00000000e+000, 0.00000000e+000,
nan, nan]]])
>>> type(a)
<class 'numpy.ndarray'>
>>> a.dtype
dtype('float64')
>>> a.shape
(2, 3, 5)
>>>
其中<class 'numpy.ndarray'>表示:a是ndarray数组对象。dtype('float64')表示:所有元素的类型是64位(8byte)的浮点型。(2, 3, 5)是个元组,表示数组的形状是三维数组空间。
在ndarray构造方法中的dtype参数指明了数组元素的数据类型,在以上举例中使用float参数指明数组元素是64位浮点型。若使用int参数,则表示数组元素是32位或64位整型。
2.利用其它方法创建数组:
- np.array(collection),collection可以是列表或元组
使用array函数从常规Python列表或元组创建数组。 根据序列中元素的类型推导所得数组的类型。
>>> import numpy as np
>>> a = np.array([(1.5,2,3), (4,5,6)])
>>> a
array([[1.5, 2. , 3. ],
[4. , 5. , 6. ]])
>>> type(a)
<class 'numpy.ndarray'>
>>> a.dtype
dtype('float64')
>>> a.shape
(2, 3)
>>>
- np.arange(开始值, 终值, 步长)
为了创建数字序列,NumPy提供了arange()函数,该函数类似于Python内置range(),但是返回一个数组,注意不包括终值。
>>> a = np.arange( 10, 30, 5 )
>>> a
array([10, 15, 20, 25])
>>> type(a)
<class 'numpy.ndarray'>
>>> a.dtype
dtype('int64')
>>> a.shape
(4,) # 意思是一维数组,数组中有4个元素
>>> b = np.arange( 0, 2, 0.3 ) # 它接受float参数
>>> b
array([0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8])
>>> type(b)
<class 'numpy.ndarray'>
>>> b.dtype
dtype('float64')
>>> b.shape
(7,)
>>>
- np.linspace(开始值, 终值, 元素个数)
默认包括终值,可以使用endpoint设置是否包括终值。当arange()与浮点参数一起使用时,由于有限的浮点精度,通常无法预测获得的元素数量。 出于这个原因,通常最好使用函数linspace()来接收所需数量的元素作为参数,而不是使用步长:
>>> import numpy as np
>>> from numpy import pi
>>> a = np.linspace( 0, 2, 9 ) # 从0到2的9个数字
>>> a
array([0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.5 , 1.75, 2. ])
>>> x = np.linspace( 0, 2*pi, 100 ) # 有助于估算多点的函数,从0到2*pi的100个数字
>>> f = np.sin(x)
>>> f
array([ 0.00000000e+00, 6.34239197e-02, 1.26592454e-01, 1.89251244e-01,
2.51147987e-01, 3.12033446e-01, 3.71662456e-01, 4.29794912e-01,
4.86196736e-01, 5.40640817e-01, 5.92907929e-01, 6.42787610e-01,
6.90079011e-01, 7.34591709e-01, 7.76146464e-01, 8.14575952e-01,
8.49725430e-01, 8.81453363e-01, 9.09631995e-01, 9.34147860e-01,
9.54902241e-01, 9.71811568e-01, 9.84807753e-01, 9.93838464e-01,
9.98867339e-01, 9.99874128e-01, 9.96854776e-01, 9.89821442e-01,
9.78802446e-01, 9.63842159e-01, 9.45000819e-01, 9.22354294e-01,
8.95993774e-01, 8.66025404e-01, 8.32569855e-01, 7.95761841e-01,
7.55749574e-01, 7.12694171e-01, 6.66769001e-01, 6.18158986e-01,
5.67059864e-01, 5.13677392e-01, 4.58226522e-01, 4.00930535e-01,
3.42020143e-01, 2.81732557e-01, 2.20310533e-01, 1.58001396e-01,
9.50560433e-02, 3.17279335e-02, -3.17279335e-02, -9.50560433e-02,
-1.58001396e-01, -2.20310533e-01, -2.81732557e-01, -3.42020143e-01,
-4.00930535e-01, -4.58226522e-01, -5.13677392e-01, -5.67059864e-01,
-6.18158986e-01, -6.66769001e-01, -7.12694171e-01, -7.55749574e-01,
-7.95761841e-01, -8.32569855e-01, -8.66025404e-01, -8.95993774e-01,
-9.22354294e-01, -9.45000819e-01, -9.63842159e-01, -9.78802446e-01,
-9.89821442e-01, -9.96854776e-01, -9.99874128e-01, -9.98867339e-01,
-9.93838464e-01, -9.84807753e-01, -9.71811568e-01, -9.54902241e-01,
-9.34147860e-01, -9.09631995e-01, -8.81453363e-01, -8.49725430e-01,
-8.14575952e-01, -7.76146464e-01, -7.34591709e-01, -6.90079011e-01,
-6.42787610e-01, -5.92907929e-01, -5.40640817e-01, -4.86196736e-01,
-4.29794912e-01, -3.71662456e-01, -3.12033446e-01, -2.51147987e-01,
-1.89251244e-01, -1.26592454e-01, -6.34239197e-02, -2.44929360e-16])
>>>
- np.reshape()
转换数组的规模但不更改其中的数据,常搭配arange或lispace使用。reshape()方法的用途是在数组元素数量不变的情况下,重新定义数组形状。
>>> a = np.arange(6) # 一维数组
>>> print(a)
[0 1 2 3 4 5]
>>> b = np.arange(12).reshape(4,3) # 二维数组
>>> print(b)
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
>>> >>> c = np.arange(24).reshape(2,3,4) # 三维数组
>>> print(c)
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
>>>
如果数组太大而无法打印,NumPy会自动跳过数组的中心部分,仅打印角点:
>>> print(np.arange(10000).reshape(100,100))
[[ 0 1 2 ... 97 98 99]
[ 100 101 102 ... 197 198 199]
[ 200 201 202 ... 297 298 299]
...
[9700 9701 9702 ... 9797 9798 9799]
[9800 9801 9802 ... 9897 9898 9899]
[9900 9901 9902 ... 9997 9998 9999]]
>>>
- np.zeros()
生成零矩阵(矩阵属于数组)。能够在构造数组时高效填充各种初值是NumPy的另一个方便之处,使用全0、全1、各种规则序列和随机数构造数组。
>>> x0 = np.zeros(12).reshape((3,4)) # 生成3行4列全0数组
>>> print(x0)
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
>>>
- np.ones()
生成全1矩阵
>>> x1 = np.ones(15).reshape((5,3)) # 生成5行3列全1数组
>>> print(x1)
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
>>>
zeros和 ones方法用来构造全0和全1数组,通常会和 reshape方法合用以确定数组形状 。
- np.identity()
生成单位矩阵。单位矩阵是在主对角线上带有1的正方形矩阵。
>>> i = np.identity(3)
>>> print(i)
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
>>>
- np.eye(N, M=None)
生成矩形矩阵(N,M),对角线的地方为1,其余的地方为0。N:int型,表示的是输出的行数;M:int型,可选项,输出的列数,如果没有就默认为N。
>>> d = np.eye(2,3)
>>> print(d)
[[1. 0. 0.]
[0. 1. 0.]]
>>> e = np.eye(3)*2.5
>>> print(e)
[[2.5 0. 0. ]
[0. 2.5 0. ]
[0. 0. 2.5]]
>>>
identity函数和 eye函数的区别在于,identity只能创建方阵。
3.使用随机数列创建数组
可以产生各种随机数序列也是NumPy的优势之一,random模块包含常用随机数生成函数:
- seed : 确定随机数生成器的种子
- permutation : 返回一个序列的随机排列或返回一个随机排列的范围
- stuffle : 对一个序列进行随机排序
- binomial : 产生二项分布的随机数
- normal : 产生正态(高斯)分布的随机数
- beta : 产生beta分布的随机数
- chisquare : 产生卡方分布的随机数
- gamma : 产生gamma分布的随机数
- uniform : 产生在[0,1]中均匀分布的随机数
生成标准随机数数组:
>>> xr = np.random.rand(2,3)
>>> print(xr)
[[0.75597145 0.90531457 0.78827221]
[0.42378164 0.95195487 0.98037761]]
>>>
函数说明:numpy.random.rand(d0, d1, ..., dn),创建给定形状的随机值数组,并使用[0,1)上均匀分布的随机样本传播给它,不包括1。
参数 : d0, d1, ..., dn : int -- 输出的形状。
生成标准正态分布的随机数数组:
>>> xrn = np.random.randn(6,4)
>>> print(xrn)
[[ 0.33464149 1.44459451 0.90211582 -0.59252553]
[ 0.19690371 -0.79955181 -0.66183452 -0.81950332]
[ 0.014866 -0.01423318 -0.70595167 -2.06465902]
[ 0.02254244 0.68077767 -0.74620655 1.56023268]
[-0.90390519 1.0697601 0.08498025 1.97195305]
[-1.34379536 0.40044248 0.9499918 0.29732109]]
>>>
函数说明:numpy.random.randn(d0, d1, ..., dn),从“标准正态”分布中返回一个或多个样本。标准正态分布是以0为均数、以1为标准差的正态分布,随机样本基本上取值主要在-1.96 ~ +1.96之间,当然也不排除存在较大值的情形,只是概率较小而已。
参数 : d0, d1, ..., dn : int(可选) -- 输出的形状。如果未提供任何参数,则返回单个Python浮点数。
生成指定均值和标准差的正太分布的随机数数组:
>>> xrns = np.random.normal(1,2,(2,3))
>>> print(xrns)
[[-0.31586191 0.16185784 2.1259619 ]
[-0.07981476 0.9827251 2.53626426]]
>>>
函数说明:numpy.random.normal(loc=0.0, scale=1.0, size=None)
参数:loc:float -- 概率分布的均值,对应着整个分布的中心;
scale:float -- 概率分布的标准差,对应分布的宽度,scale越大,分布的曲线越矮胖,scale越小,曲线越高瘦;
size:int or tuple of ints(或者整数元组) -- 输出的值赋在shape里,默认为None。
在指定边界中生成指定均值的随机数数组:
>>> xru = np.random.uniform(1,10,10)
>>> print(xru)
[5.17367288 7.69298272 1.78530786 7.81860516 6.87571567 3.34691674
1.84101405 8.8976795 8.10280517 6.50217056]
>>>
函数说明:numpy.random.uniform(low,high,size),从一个均匀分布[low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high。
参数:low -- 采样下界,float类型,默认值为0;
high -- 采样上界,float类型,默认值为1;
size -- 输出样本数目。
按指定数量生成指定边界的随机整数序列:
>>> xri = np.random.randint(1,10,(2,5))
>>> print(xri)
[[2 9 3 3 6]
[1 6 1 3 6]]
>>>
函数说明:numpy.random.randint(low, high=None, size=None, dtype='l'),返回一个随机整型序列,范围从低(包括)到高(不包括),即[low, high)。如果没有写参数high的值,则返回[0,low)的值。
参数:low: int -- 生成的数值最低要大于等于low,(hign = None时,生成的数值要在[0, low)区间内);
high: int (可选) -- 如果使用这个值,则生成的数值在[low, high)区间;
size: int or tuple of ints(可选) -- 输出随机数的数量;
dtype: dtype(可选) -- 指定输出类型。
4.矩阵转置:
- numpy.ndarray.T
返回转置数组。进行矩阵运算时,经常要用数组转置。
>>> import numpy as np
>>> x = np.arange(1,5,dtype = np.float64).reshape(2,2)
>>> x
array([[1., 2.],
[3., 4.]])
>>> x.T # 二维数组的转置使得二维数组的行列发生对换
array([[1., 3.],
[2., 4.]])
>>> y = np.arange(1,5,dtype = np.float64)
>>> y
array([1., 2., 3., 4.])
>>> y.T # 一维数组的转置保持不变
array([1., 2., 3., 4.])
>>>
- numpy.transpose(a, axes=None)
使用轴交换来实现多维数组的转置。
参数: a -- 输入数组
axes(可选) -- 一个整数数列,默认情况下,反转维度,否则根据给定的值对轴进行交换。
返回值:ndarray -- 一个已交换了轴的数组
二维数组转置:
对于一个两行两列的二维数组,通过数组下标访问数据单元,给每个单元赋值,通过以下操作进行:
a[0][0] = 0
a[0][1] = 1
a[1][0] = 2
a[1][1] = 3
指定第一个方括号[]为0轴,第二个方括号[]为1轴,则建立了以0轴为水平坐标、以1轴为垂直坐标的0-1坐标系,如下图所示:
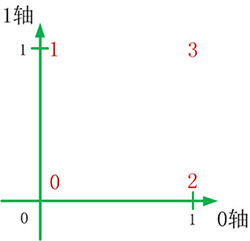
>>> x = np.arange(4).reshape((2,2)) # 创建数组对象,按照0-1坐标系初始化数组单元的值
>>> x
array([[0, 1],
[2, 3]])
>>> np.transpose(x,(0,1)) # axes参数为(0,1)时,表示按照原坐标轴改变序列,即保持不变,所以最后的结果不变。
array([[0, 1],
[2, 3]])
>>> np.transpose(x) # 不指定axes参数时,默认是数组转置
array([[0, 2],
[1, 3]])
>>> np.transpose(x,(1,0)) # axes参数为(1,0)时,表示交换 ‘0轴’ 和 ‘1轴’,其结果是数组转置。
array([[0, 2],
[1, 3]])
>>>
转置后,通过数组下标表达的单元数据为:
a[0][0] -> 0
a[0][1] -> 2
a[1][0] -> 1
a[1][1] -> 3
0轴 和 1轴 交换后的1-0坐标系,如下图所示:
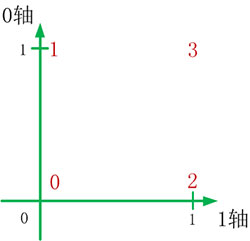
无论何时,记住第一个方括号[]及下标代表0轴 ,第二个方括号[]及下标代表1轴。
三维数组转置:
>>> import numpy as np
>>> y = np.arange(16).reshape(2,2,4) # 第一个参数表示第几维,第二个参数表示该维第几行,第三个参数表示该行第几列
>>> y # 构建的数组对象可以理解为2个2*4的矩阵
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
>>>
三维数组对象创建并初始化后,其三维坐标系0-1-2表示如下:
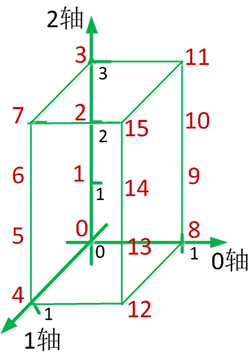
针对三维数组对象分别进行不同形式的转置可通过坐标轴完成:
>>> np.transpose(y, (0,1,2)) # 坐标轴0-1-2没有变化,数组对象y保持不变
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]]])
>>> np.transpose(y, (1,0,2)) # 坐标轴0与坐标轴1进行了交换,数组对象y发生变化
array([[[ 0, 1, 2, 3],
[ 8, 9, 10, 11]],
[[ 4, 5, 6, 7],
[12, 13, 14, 15]]])
>>> np.transpose(y, (2,1,0)) # 坐标轴0与坐标轴2进行了交换,数组对象y发生变化
array([[[ 0, 8],
[ 4, 12]],
[[ 1, 9],
[ 5, 13]],
[[ 2, 10],
[ 6, 14]],
[[ 3, 11],
[ 7, 15]]])
>>>
坐标轴0与坐标轴1交换后的1-0-2坐标系如下所示:
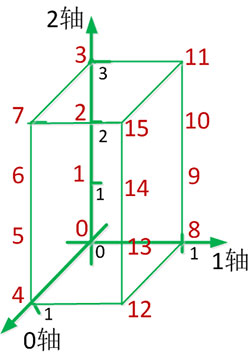
坐标轴0与坐标轴2交换后的2-1-0坐标系如下所示:
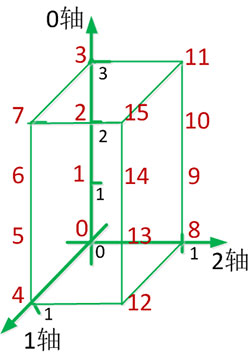
通过分析数组对象y的结果可看出,0轴始终代表最高维数,即2个2x4矩阵或4个2x2矩阵,只不过数据单元发生了变化。
5. 索引与切片
ndarray数组对象的内容可以通过索引或切片来访问和修改,其对象中的元素索引从零开始。
- 索引:选择数组的元素,以
[]表示; - 切片:带有
冒号(:)的索引表示切片,用来访问一定范围内的元素,冒号前表示起始索引,冒号后表示终止索引,但不包含终止索引所对应的元素; - 一维数组对象的索引与Python的列表索引类似。
索引的引用是从0到size-1,而维度的间隔使用逗号分隔。
>>> a = np.array([[11,12,13,14],[21,22,23,24],[31,32,33,34]]) # 构造3行4列的数组
>>> a
array([[11, 12, 13, 14],
[21, 22, 23, 24],
[31, 32, 33, 34]])
>>> a[:2, 1:3] # 从第1行到第2行,从第2列到第3列做了切片,切片的结果还是矩阵数组
array([[12, 13],
[22, 23]])
利用索引数组和start:end:step方式获得子集
>>> b = np.array([[11,12,13,14,15],[21,22,23,24,25],[31,32,33,34,35],[41,42,43,44,45]]) # 构建4行5列的数组
>>> b
array([[11, 12, 13, 14, 15],
[21, 22, 23, 24, 25],
[31, 32, 33, 34, 35],
[41, 42, 43, 44, 45]])
>>> b[np.arange(4), 0:5:2] # 索引视图
array([[11, 13, 15],
[21, 23, 25],
[31, 33, 35],
[41, 43, 45]])
>>> b[np.arange(4), 0:5:2] = 88 # 更新索引视图的值
>>> b
array([[88, 12, 88, 14, 88],
[88, 22, 88, 24, 88],
[88, 32, 88, 34, 88],
[88, 42, 88, 44, 88]])
>>>
6.遍历与推导式(comprehensions)
需要访问数组的元素时,通常会考虑使用for循环遍历数组。应当认识到,对于规模巨大的矩阵,遍历是一种很低效的方法,这时可以利用推导式较大程度的简化代码。
推导式是可以从一个数据序列构建另一个新的数据序列的结构体:
- 列表(list)推导式
- 字典(dict)推导式
- 集合(set)推导式
列表推导式: 通过列表推导式可以对列表中的所有元素都进行统一的操作来获得一个全新的列表。
>>> w = np.arange(5, 9)
>>> w
array([5, 6, 7, 8])
>>> b = [x+2 for x in w] # 列表推导式
>>> b
[7, 8, 9, 10]
>>> a = np.arange(9).reshape(3, 3)
>>> [(x, y) for x, y in np.ndindex(a.shape)] # 列表推导式
[(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)]
>>>
字典推导式: 通过字典推导式来创建一个新字典,字典推导式的括号使用花括号。
>>> a = np.arange(9)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8])
>>> { "s"+str(i):i for i in a } # 字典推导式
{'s0': 0, 's1': 1, 's2': 2, 's3': 3, 's4': 4, 's5': 5, 's6': 6, 's7': 7, 's8': 8}
>>>
集合推导式: 集合推导式与字典推导式类似,其内只有值而不是键值对。
>>> a = np.arange(1, 6)
>>> a
array([1, 2, 3, 4, 5])
>>> {i**2 for i in a if i%2==1} # 集合推导式
{1, 9, 25}
>>>
三、基本操作
数组上的算术运算按元素进行。 创建一个新数组,并用结果填充。NumPy能够用运算符复用方式和函数方式进行矩阵计算。
>>> import numpy as np
>>> x = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]],dtype = np.float64)
>>> x
array([[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.]])
>>> y = np.arange(51,63,dtype = np.float64).reshape(3,4)
>>> y
array([[51., 52., 53., 54.],
[55., 56., 57., 58.],
[59., 60., 61., 62.]])
>>> x + y # 矩阵加,使用运算符
array([[52., 54., 56., 58.],
[60., 62., 64., 66.],
[68., 70., 72., 74.]])
>>> np.add(x, y) # 矩阵加,使用函数
array([[52., 54., 56., 58.],
[60., 62., 64., 66.],
[68., 70., 72., 74.]])
>>> y - x # 矩阵减,使用运算符
array([[50., 50., 50., 50.],
[50., 50., 50., 50.],
[50., 50., 50., 50.]])
>>> np.subtract(y, x) # 矩阵减,使用函数
array([[50., 50., 50., 50.],
[50., 50., 50., 50.],
[50., 50., 50., 50.]])
>>> x * y # 矩阵乘,使用运算符
array([[ 51., 104., 159., 216.],
[275., 336., 399., 464.],
[531., 600., 671., 744.]])
>>> np.multiply(x, y) # 矩阵乘,使用函数
array([[ 51., 104., 159., 216.],
[275., 336., 399., 464.],
[531., 600., 671., 744.]])
>>> x / y # 矩阵除,使用运算符
array([[0.01960784, 0.03846154, 0.05660377, 0.07407407],
[0.09090909, 0.10714286, 0.12280702, 0.13793103],
[0.15254237, 0.16666667, 0.18032787, 0.19354839]])
>>> np.divide(x, y) # 矩阵除,使用函数
array([[0.01960784, 0.03846154, 0.05660377, 0.07407407],
[0.09090909, 0.10714286, 0.12280702, 0.13793103],
[0.15254237, 0.16666667, 0.18032787, 0.19354839]])
>>>
逐元素求平方根:
>>> np.sqrt(x) # 使用numpy函数,以元素为单位返回数组的正平方根
array([[1. , 1.41421356, 1.73205081, 2. ],
[2.23606798, 2.44948974, 2.64575131, 2.82842712],
[3. , 3.16227766, 3.31662479, 3.46410162]])
>>>
矩阵内积相乘:
>>> v = np.array([2,3,4,5]) # 创建向量
>>> w = np.array([5,6,7,8]) # 创建向量
>>> v.dot(w) # 向量 乘 向量,使用向量的点积函数
96 # 两个向量相乘,对向量而言,无论转置与否,结果相同
>>> np.dot(v, w) # 向量 乘 向量,使用numpy的点积函数
96
>>> x.dot(v) # 矩阵 乘 向量,使用矩阵的点积函数
array([ 40., 96., 152.])
>>> np.dot(x, v) # 矩阵 乘 向量,使用numpy的点积函数
array([ 40., 96., 152.]) # 矩阵与向量相乘,相乘的法则为:np.dot([m,n],[n])的结果为[m]
>>> y.T
array([[51., 55., 59.], # 矩阵y的转置
[52., 56., 60.],
[53., 57., 61.],
[54., 58., 62.]])
>>> x.dot(y.T) # 矩阵x 与矩阵y 相乘
array([[ 530., 570., 610.],
[1370., 1474., 1578.],
[2210., 2378., 2546.]])
>>> np.dot(x, y.T) # 矩阵x 与矩阵y 相乘
array([[ 530., 570., 610.],
[1370., 1474., 1578.],
[2210., 2378., 2546.]])
>>> np.dot(y.T, x) # 矩阵x 与矩阵y 相乘,左右交换结果不同
array([[ 857., 1022., 1187., 1352.],
[ 872., 1040., 1208., 1376.],
[ 887., 1058., 1229., 1400.],
[ 902., 1076., 1250., 1424.]])
>>>
求矩阵和:
>>> np.sum(x) # 求矩阵和,求矩阵所有元素的总和
78.0
>>> np.sum(x, axis = 0) # 由参数axis = 0表明按0轴方向求和(即按列求和)
array([15., 18., 21., 24.])
>>> np.sum(x, axis = 1) # 由参数axis = 1表明按1轴方向求和(即按行求和)
array([10., 26., 42.])
>>>
以上代码中,numpy的函数sum的参数axis 表达了运算方向。如果ndarray数组有n个维度,则该数组的秩(rank)为n,其含义可理解为数组有n个计算方向,可以称之为轴(axis),其表达了维度索引值的变化方向。对于一个二维数组,维度是2,第0维是行,第1维是列,即包含 0 和 1 两个轴(axis),其中axis = 0是指“按第0维索引(行索引)变化”方向,而axis = 1是指“按第1维索引(列索引)变化”方向。其图示如下:
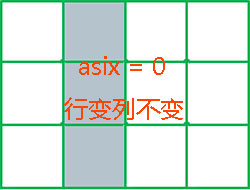 axis = 0
axis = 0 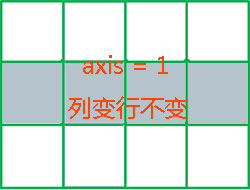 axis = 1
axis = 1
统计、排序与搜索:
NumPy提供了简单的函数能够完成统计、排序与搜索任务。
- numpy.amin(a, axis=None, out=None, keepdims=, initial=, where=)
返回数组的最小值或沿轴的最小值。
>>> a = np.array([[23,17,85],[24,38,63],[12,4,19]])
>>> a
array([[23, 17, 85],
[24, 38, 63],
[12, 4, 19]])
>>> np.amin(a) # 对整个数组调用amin()函数
4
>>> np.amin(a, axis=1) # 在axis=1方向,调用amin()函数
array([17, 24, 4])
>>>
- numpy.amax(a, axis=None, out=None, keepdims=)
返回数组的最大值或沿轴的最大值。
>>> np.amax(a, axis=0) # 在axis=0方向,调用amax()函数
array([24, 38, 85])
>>>
- numpy.ptp(a, axis=None, out=None, keepdims=)
求沿轴的值范围(最大值-最小值)。函数的名称来自“ peak to peak”的缩写。
>>> np.ptp(a) # 对整个数组调用 ptp() 函数
81
>>> np.ptp(a, axis=1) # 在axis=1方向,调用 ptp() 函数
array([68, 39, 15])
>>> np.ptp(a[:,2]) # 在第3列,调用 ptp() 函数
66
>>>
- numpy.ndarray.sort(axis=-1, kind='quicksort', order=None)
就地对数组进行排序。
>>> a = np.array([[1,4], [3,1]])
>>> a.sort(axis=1)
>>> a
array([[1, 4],
[1, 3]])
>>> a.sort(axis=0)
>>> a
array([[1, 3],
[1, 4]])
- numpy.sort(a, axis=-1, kind='quicksort', order=None)
返回数组的排序副本。
>>> a = np.array([[1,4],[3,1]])
>>> np.sort(a) #沿最后一个轴排序
array([[1, 4],
[1, 3]])
>>> np.sort(a, axis=None) #对扁平化数组进行排序
array([1, 1, 3, 4])
>>> np.sort(a, axis=0) #沿第一个轴排序
array([[1, 1],
[3, 4]])
- numpy.argsort(a, axis=-1, kind='quicksort', order=None)
返回将对数组进行排序的索引。使用kind关键字指定的算法,沿着给定的轴执行间接排序。 它沿给定轴按排序顺序返回与该索引数据具有相同形状的索引数组。
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)
array([1, 2, 0])
>>> x = np.array([[0, 3], [2, 2]])
>>> x
array([[0, 3],
[2, 2]])
>>> np.argsort(x, axis=0) # 沿第一轴(0轴)排序
array([[0, 1],
[1, 0]])
>>> np.argsort(x, axis=1) # 沿最后一个轴(1轴)排序
array([[0, 1],
[0, 1]])
- numpy.lexsort(keys, axis=-1)
使用键序列执行间接稳定排序。
>>> surnames = ('Hertz', 'Galilei', 'Hertz')
>>> first_names = ('Heinrich', 'Galileo', 'Gustav')
>>> ind = np.lexsort((first_names, surnames)) # 对名称进行排序:首先按姓氏,然后按名称。
>>> ind
array([1, 2, 0])
- numpy.searchsorted(a, v, side='left', sorter=None)
查找应在其中插入元素时保持顺序的索引。
>>> np.searchsorted([1,2,3,4,5], 3)
2
NumPy中常用的统计函数还有:
- numpy.percentile(a, q, axis=None, out=None, overwrite_input=False, interpolation='linear', keepdims=False)
计算沿指定轴的数据的第q个百分位数。返回数组元素的第q个百分点。该函数返回占某个百分比的元素的上限。如果q = 50,此函数与中位数相同;如果q = 0,则与最小值相同;如果q = 100,则与最大值相同。
>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10, 7, 4],
[ 3, 2, 1]])
>>> np.percentile(a, 50) # 50%的分位数,即a中排序之后的中位数。
3.5
>>> np.percentile(a, 50, axis=0) # 0轴方向50%的分位数。
array([6.5, 4.5, 2.5])
>>> np.percentile(a, 50, axis=1) # 1轴方向50%的分位数。
array([7., 2.])
>>> np.percentile(a, 50, axis=1, keepdims=True) # 1轴方向50%的分位数,保持维度不变
array([[7.],
[2.]])
>>>
- numpy.median(a, axis=None, out=None, overwrite_input=False, keepdims=False)
计算沿指定轴的中值。返回数组元素的中值。
>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10, 7, 4],
[ 3, 2, 1]])
>>> np.median(a) # a的中值
3.5
>>> np.median(a, axis=0) # 0轴方向的中值
array([6.5, 4.5, 2.5])
>>> np.median(a, axis=1) # 1轴方向的中值
array([7., 2.])
- numpy.mean(a, axis=None, dtype=None, out=None, keepdims=)
沿指定轴计算算术平均值。返回数组元素的平均值。 默认情况下,平均值取自展平的数组,否则取自指定的轴。 float64中间值和返回值用于整数输入。
>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10, 7, 4],
[ 3, 2, 1]])
>>> np.mean(a) # a的平均值
4.5
>>> np.mean(a, axis=0) # 0轴方向的平均值
array([6.5, 4.5, 2.5])
>>> np.mean(a, axis=1) # 1轴方向的平均值
array([7., 2.])
>>>
- numpy.average(a, axis=None, weights=None, returned=False)
计算沿指定轴的加权平均值。若无加权参数,则与mean()函数一致。
>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10, 7, 4],
[ 3, 2, 1]])
>>> np.average(a)
4.5
>>> np.average(a, axis=0, weights=[1/3, 2./3])
array([5.33333333, 3.66666667, 2. ])
>>> np.average(a, axis=1, weights=[1, 2./3, 1/3])
array([8. , 2.33333333])
>>>
- numpy.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=)
计算沿指定轴的标准偏差。返回数组元素的标准偏差。 默认情况下,将为展平数组计算标准偏差,否则将在指定轴上计算。其中的ddof表示Delta自由度,默认情况下,ddof为零,调用时,可手动设置ddof = 1。
>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10, 7, 4],
[ 3, 2, 1]])
>>> np.std(a, ddof=1)
3.391164991562634
>>> np.std(a, axis=0)
array([3.5, 2.5, 1.5])
>>> np.std(a, axis=1)
array([2.44948974, 0.81649658])
>>>
- numpy.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=)
计算沿指定轴的方差。返回数组元素的方差。 默认情况下,将为展平数组计算方差,否则将在指定轴上计算方差。其中的ddof表示Delta自由度,默认情况下,ddof为零,调用时,可手动设置ddof = 1。
>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10, 7, 4],
[ 3, 2, 1]])
>>> np.var(a, ddof=1)
11.5
>>> np.var(a, axis=0)
array([12.25, 6.25, 2.25])
>>> np.var(a, axis=1)
array([6. , 0.66666667])
>>>
- numpy.ndarray.min(axis=None, out=None, keepdims=False)
沿给定轴返回最小值。
- numpy.ndarray.max(axis=None, out=None, keepdims=False)
沿给定轴返回最大值。
- numpy.argmin(a, axis=None, out=None) 或 numpy.ndarray.argmin(axis=None, out=None)
沿a的给定轴返回最小值的索引。
- numpy.argmax(a, axis=None, out=None) 或 numpy.ndarray.argmax(axis=None, out=None)
沿给定轴返回最大值的索引。
- numpy.cumsum(a, axis=None, dtype=None, out=None)
返回沿给定轴的元素的累计和。
- numpy.cumprod(a, axis=None, dtype=None, out=None)
返回沿给定轴的元素的累计积。
博文最后更新时间: