任务一要求：

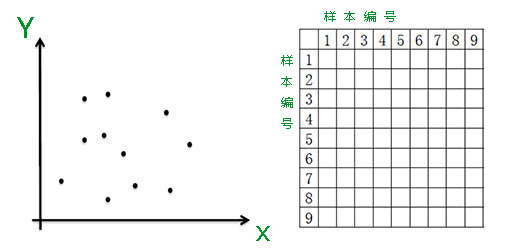
• 建立X-Y坐标系；
• 生成100个样本的X坐标值与Y坐标值，如图所示；
• 求任意两点间的距离

任务二要求：使用k-means

1. 随机选取两个点作为初始类中心；
2. 求各点至类中心的距离；
3. 将各点归为距离其最近的类中心所属类；
4. 计算各类点坐标值的均值作为新类中心；
5. 判断：若类中心不再变化或达到迭代次数，即结束，否则返回第2项继续。

k-means简介：其称为k均值聚类算法（k-means clustering algorithm），是一种迭代求解的聚类分析算法，其步骤是随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程，聚类就是一种发现这种内在结构的技术，聚类技术经常被称为无监督学习。

任务一步骤：

第一步：生成100个样本

import numpy as np
n = 100
x = np.linspace(1, 100, n)     # 生成100个样本的X坐标值
y = np.linspace(101, 200, n)   # 生成100个样本的Y坐标值

第二步：生成100行100列的全零矩阵

distance = np.zeros([n, n])    # 生成n行n列的全零矩阵

第三步：求各样本之间的距离，并存储到矩阵中

for i in range(n)
     for j in range(n)
          distance[i, j] = np.sqrt((x[i]-x[j])**2 + (y[i]-y[j])**2) # 欧式距离公式

任务二步骤：

第一步：选中心

import numpy as np
n = 100                          # 样本个数
k = 2                            # 指定k为两类
x = np.linspace(1, 100, n)       # 生成100个样本的X坐标值
y = np.linspace(101, 200, n)     # 生成100个样本的Y坐标值
dist = np.zeros([n, k+1])        # 生成100行3列的全零矩阵
center0 = np.array([x[0], y[0]]) # 选取x[0]、y[0]的点作为第一个类中心
center1 = np.array([x[1], y[1]]) # 选取x[1]、y[1]的点作为第二个类中心

第二步：求距离

for i in range(n):
    dist[i, 0] = np.sqrt((x[i]-center0[0])**2 + (y[i]-center0[1])**2) # 第i个点到第一个类中心的距离
    dist[i, 1] = np.sqrt((x[i]-center1[0])**2 + (y[i]-center1[1])**2) # 第i个点到第二个类中心的距离

第三步：归类

for i in range(n):
    dist[i, 0] = np.sqrt((x[i]-center0[0])**2 + (y[i]-center0[1])**2)
    dist[i, 1] = np.sqrt((x[i]-center1[0])**2 + (y[i]-center1[1])**2)
    dist[i, k] = dist[i, :2].argmin()   # 归类：求矩阵第i行前两列的最小值的索引(位置)，存入矩阵第3列

第四步：求新类中心

index0 = dist[:, k] == 0    # 筛选第1类样本，将矩阵第3列与0比较，形成布尔值数组index0(ndarray)
index1 = dist[:, k] == 1    # 筛选第2类样本，将矩阵第3列与1比较，形成布尔值数组index1(ndarray)
center0_new = np.array([x[index0].mean(), y[index0].mean()])   # 通过“逻辑值索引”x[index0]、y[index0]取出对应为true的各1类点样本并求均值，形成1类样本的新的中心。
center1_new = np.array([x[index1].mean(), y[index1].mean()])   # 通过“逻辑值索引”x[index1]、y[index1]取出对应为true的各2类点样本并求均值，形成2类样本的新的中心。

第五步：判定是否结束

while True:
    for i in range(n):
        dist[i, 0] = np.sqrt((x[i]-center0[0])**2 + (y[i]-center0[1])**2)
        dist[i, 1] = np.sqrt((x[i]-center1[0])**2 + (y[i]-center1[1])**2)
        dist[i, k] = dist[i, :2].argmin()

    index0 = dist[:, k] == 0
    index1 = dist[:, k] == 1
    center0_new = np.array([x[index0].mean(), y[index0].mean()])
    center1_new = np.array([x[index1].mean(), y[index1].mean()])
    # 5. 判定是否结束，如果类中心无改变，即结束，否则继续。
    if sum(center0 == center0_new) + sum(center1 == center1_new) == 4:
        break
    center0 = center0_new   # 更新类中心
    center1 = center1_new