深度学习是机器学习的一个子领域，它是一组受大脑结构和功能启发的算法。深度学习是人工智能领域的热搜议题。而TensorFlow是作为深度学习的工具之一。

TensorFlow是Google创建并用于设计，构建和训练深度学习模型的机器学习框架。 可以使用TensorFlow库来进行数值计算，虽然看起来似乎并不特殊，但是这些计算是通过数据流图完成的。 在这些图中，节点表示数学运算，而边沿表示数据，通常是多维数据数组或张量，在这些边沿之间进行通信。

TensorFlow名字中的含义：名称“TensorFlow”源自神经网络对多维数据数组或张量执行的操作！ 它实际上是张量流。 目前，这只是张量所需的所有知识，接下来，将更深入地了解这一点！张量是在深度学习中表示数据的标准方式。简单来说，张量就是多维数组，是二维表（矩阵）到更高维度的扩展。

在TensorFlow中，将计算看作数据流通，如图1所示。即在这个图中，节点表示操作(如加法或乘法等)，而边表示数据(张量)流经系统。

图1 TensorFlow的数据流图

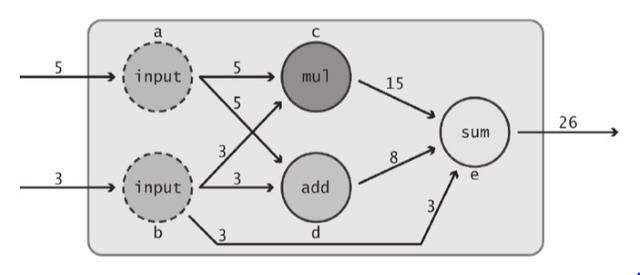
TensorFlow是基于数据流图的数值计算的软件框架。侧重于深度神经网络，为表达和实现机器学习算法提供了接口。TensorFlow的核心是用C++语言编写的，用于执行计算图。有Python前端语言的接口，供表达计算图，相对容易的表达模型。

一、安装TensorFlow

1.创建虚拟环境

根据当前环境，安装virtualenv：

$ pip install virtualenv

在主目录下创建mytf文件夹，并进入mytf，使用virtualenv 命令创建Python 虚拟环境:

$ cd ~
$ mkdir mytf
$ cd mytf
$ virtualenv venv

使用以下命令来激活该虚拟环境：

$ source venv/bin/activate

激活虚拟环境的命令会修改命令行提示符，加入环境名：

(venv) $

最后，使用以下命令退出虚拟环境：

(venv) $ deactivate

现在命令行提示符恢复正常：

$

2. 在虚拟环境下安装tensorflow：

 (venv) $ pip install tensorflow

这条命令会在虚拟环境中安装 TensorFlow，而且不会影响当前机器上的其他已安装的包。

使用国内阿里云镜像站点安装tensorflow，以便快速安装：

 (venv) $ pip install tensorflow -i https://mirrors.aliyun.com/pypi/simple/

3. TensorFlow的使用初步：

TensorFlow提供了适用于Python、C ++、Haskell、Java、Go、Rust的API，并且还有用于R的第三方程序包tensorflow。在本博文中，将下载的TensorFlow版本，能够使用Python编写深度学习项目的代码。

现在，已经完成了安装过程，是时候通过将别名tf导入到工作区中来仔细检查是否已正确安装TensorFlow：

import tensorflow as tf

请注意，在上面的代码行中使用的别名tf是一种约定，用于确保：一方面与在数据科学项目中使用TensorFlow的其他开发人员保持一致，另一方面并与开源TensorFlow项目保持一致。

简单的一个案例是将“Hello”与“World”两个单词组合起来，然后输出“Hello World”这个短语。

二、张量介绍

为了更好地理解张量，最好具有线性代数和矢量运算的一些应用知识。TensorFlow中将张量实现为多维数据数组，为了完全掌握张量及其在机器学习中的使用，可能需要进一步了解。

平面向量

在研究平面向量之前，最好先修订一下“向量”的概念； 向量是矩阵的特殊类型，是数字的矩形阵列。 因为向量是数字的有序集合，所以它们通常被视为列矩阵：它们只有一列和一定数量的行。 换句话说，也可以将向量视为已指定方向的标量。

请记住： 一个标量的示例是：“ 5米”或“ 60 m / sec”，而一个矢量的示例是：“向北5米”或“向东 60 m / sec”。 两者之间的区别显然是向量具有方向。 不过，到目前为止所看到的这些示例似乎与处理机器学习问题时可能遇到的向量相差很远。 这个是正常的；数学向量的长度是一个纯数字：绝对值。 另一方面，方向是相对的：相对于某些参考方向进行测量，并以弧度或度为单位。 通常会假设该方向为正，并且与参考方向成逆时针方向旋转。

图2 向量图

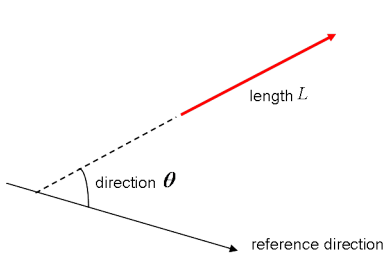
当然，在视觉上，将向量表示为箭头，如上图所示。 这意味着也可以将向量视为具有方向和长度的箭头。 方向由箭头的头部指示，而长度由箭头的长度指示。

那么，什么是平面向量？

平面向量是张量最直接的设置。 它们就像在上面所看到的常规向量一样，唯一的区别是它们位于向量空间中。 为了更好地理解这一点，从一个示例开始： 有一个2 X 1的向量。这意味着该向量属于一次配对两个的实数集。 或者，换句话说，它们是两个空间的一部分。 在这种情况下，可以用箭头或射线在坐标（x，y）平面上表示向量。

在向量的端点位于原点（0,0）的标准位置上，从此坐标平面开始工作，可以通过查看向量的第一行来得出x坐标，而在第二行中可以找到y坐标。 当然，并不总是需要保持此标准位置：向量可以在平面中平行于自身移动而不会发生变化。

请注意，类似地，对于大小为3 X 1的向量，将讨论三维空间。 可以将矢量表示为三维图形，其中的箭头指向矢量空间的位置：它们绘制在标准的x，y和z轴上。

拥有这些向量并在坐标平面上表示它们，真是太好了，但是实质上，拥有这些向量，以便可以对它们执行操作，并且可以通过将向量表示为基数或单位来有助于完成操作向量。

单位向量是大小为1的向量。 如果要将2-D或3-D矢量表示为两个或三个正交分量（例如x和y轴或z轴）的总和，则单位矢量会很方便。

而且，当谈论将一个向量表示为例如分量的和时，将会看到正在谈论的是分量向量，这是两个或多个向量，其和为给定向量。

张量

除了平面向量，协向量和线性算子也是另外两种情况，这三种情况都具有共同点：它们是张量的特定情况。 记得之前将矢量表征为已给出方向的标量。 那么，张量是物理实体的数学表示，可以用幅度和多个方向来表征。

而且，就像在3维空间中表示一个具有单个数字的标量和一个具有三个数字序列的向量一样，张量可以由3维空间中的3R数字数组表示。

此符号中的“R”表示张量的等级：这意味着在3维空间中，第二等级张量可以由3的幂2或9的数字表示。 在N维空间中，标量仍将只需要一个数，而向量将需要N个数，张量将需要N ^ R个数。 这解释了为什么经常听到标量是等级0的张量的原因：由于它们没有方向，因此可以用一个数字表示它们。

考虑到这一点，识别标量、向量和张量，并将它们分开相对容易：标量可以由单个数字表示，向量可以由有序数字集表示，张量可以由数字数组表示。

使张量如此独特的是分量和基向量的组合：基向量在参考帧之间进行一种转换，而分量以使分量和基向量之间的组合保持相同的方式进行转换。

三、理解TensorFlow

TensorFlow使用数据流图进行数值计算。

3.1 计算图

通过创建和计算相互交互的操作来实现机器学习算法，这些交互形成“计算图”。利用计算图表达复杂的功能结构。

计算图：

图是相互连接的实体的集合，称为节点（node），节点通过边（edge）相互连接。在数据流图中，边可以让数据从一个节点按指定方向流至其它节点。

TensorFlow图中的每个节点表示一个操作，可能会在输入上生成传递给其他节点的输出。计算图上的操作包含所有类型的函数，也包含更加通用的操作。

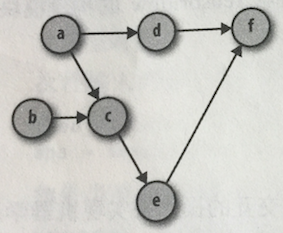
每个图有自己的节点依赖关系集合，当节点c的输入受节点a的输出时，则称节点c依赖于节点a。当两个节点通过一条边相连时，称之为直接依赖，否则称为间接依赖。上图中，节点e直接依赖于节点c，间接依赖于节点a，而独立于节点d。

3.2 图与会话

使用 TensorFlow包含两个主要步骤：① 构建图；② 执行图

构建图：

导入TensorFlow:

import tensorflow as tf

导入之后，一个空的默认图被创建了，后续创建的节点自动关联到该图上。使用tf.<operator>方法，可以创建6个节点，并赋值给一个变量。变量的内容可以看作是操作的输出，而不是操作本身。

为了兼容TensorFlow版本2.0与版本1.0，通过下列方式导入，并在程序开始部分添加代码：

import tensorflow.compat.v1 as tf
tf.compat.v1.disable_eager_execution()

使用对应的变量名来饮用操作和输出，将前三个节点定义为输出一个常量值：

a = tf.constant(5)
b = tf.constant(2)
c = tf.constant(3)

后三个节点则以两个已有的变量为输入，执行算术操作：

d = tf.multiply(a, b)
e = tf.add(c, b)
f =  tf.subtract(d, e)

节点d将节点 a和b的输出相乘；节点e将节点b和c的输出相加；节点f从节点d的输出值中减去节点e的输出值。

创建会话并运行：

完成了计算图的描述定义，就可以运行计算图，需要创建会话并执行会话：

sess = tf.Session()
outs = sess.run(f)
print("outs = {}".format(outs))